DeepSeekMath V2 By Deepseek: A Math Reasoner

DeepSeekMath-V2 - Mathematical Reasoning at its Finest

DeepSeek has released a new model. When it appeared a few hours ago, there was a surge of excitement across the community. Then came a wave of disappointment when people realized it was a math model, although a huge one with 163 shards. It cannot be installed locally by most people, except large labs or major serving engines.

There should not be disappointment. AI is not just OCR, image generation, or a new fancy large language model. Releasing a math model is genuinely innovative in a way that matters.

I am not going to install it locally because I do not have a multi-GPU cluster. Instead, I will explain why a model like this is crucial and where the industry is headed. I will go deep into what DeepSeek has introduced with Math V2, keep the language simple yet informative, and avoid unnecessary detail. So let’s get into it.

Why DeepSeekMath-V2 is a Crucial Offering

Mathematical reasoning is one of the most rigorous tests for AI. In contrast to general language tasks, mathematics demands absolute precision. Every step must be logically sound, and a single error can invalidate an entire proof. This makes it an ideal benchmark for measuring true AI reasoning capabilities.

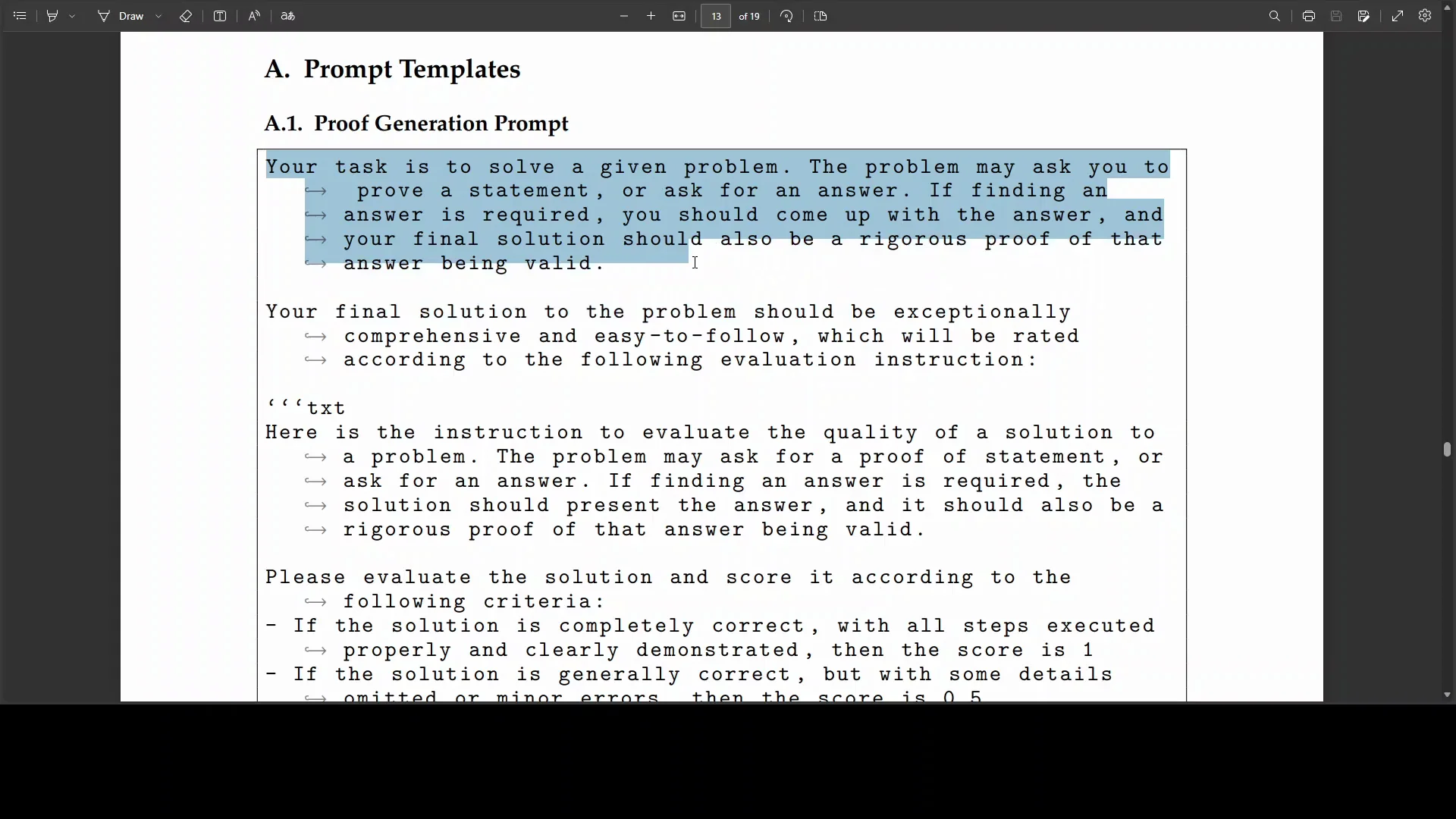
An example from their paper illustrates this clearly. The prompt template is structured and deliberate. It gives the model a task to solve a problem and, before even presenting the problem, defines at a high level what the model should do and what the final solution should look like. After that, it gives more instructions about how to proceed.

It asks the model to evaluate its solution and score it according to criteria, with additional requirements tied to the problem. It tells the model that it has the ability to rate its own solution because it is trained with reinforcement learning and verifiable rewards. The instructions ask it to reason carefully, evaluate its method, and format the final response in a specific way. At this point, the actual problem has not been given yet.

The prompt continues by outlining how to proceed, what to evaluate, how to solve, and how to present the final response. It also encourages confidence, includes a fallback plan, describes what a worst final plan might look like, and adds more instructions around evaluating the solution. Only then is the task given. That is the entire setup.

This is a master class in prompt engineering. You do not need a course or a book to learn effective prompting. Following this example is enough for deep research tasks. One key takeaway is to adopt this kind of prompt structure for coding or math tasks that require deep analysis.

Why Math Matters at the Core

Let me build the case for math. Mathematics drives progress in physics, engineering, cryptography, drug discovery, and material sciences. An AI system that advances mathematics could accelerate innovation across scientific domains, benefiting everything and everyone.

Theorem proving is not just calculating answers. It requires constructing rigorous logical arguments. That capability transfers directly to verifying software correctness, designing secure systems, and solving complex real-world problems that demand provably correct solutions. From industry to research domains, math remains a core pillar.

The Core Problem DeepSeekMath-V2 Tackles

There have been math models before, and they often focused on producing correct final answers using reinforcement learning rewards. That approach created two major issues:

• Correct answers without correct reasoning
  • A model could land on the right answer through flawed logic or lucky shortcuts.
• Proofs without rigor
  • Many mathematical problems do not require a numerical answer. They require step-by-step proofs. As a result, models produced mathematically invalid proofs with logical inconsistencies, failed to verify their own work reliably, and at times claimed incorrect proofs were valid, leading to hallucinations.

DeepSeekMath-V2 introduces a new approach. It trains AI to verify proofs without relying on reference solutions. It mirrors how mathematicians identify errors even when they do not know the final answer.

You may have seen the ongoing debates on social media saying scaling is over and large language models are at a dead end. The argument is that they try to become self-sustaining but are not mirroring intelligence. Humans identify errors in uncertainty. This model targets that ability.

Architecture Overview: A Dual-System Approach

The architecture uses a dual-system design with an additional generator.

• Verifier

  • Trained to analyze proofs and identify specific issues.
  • Assigns scores: 1 for completely rigorous, 0.5 for omissions, and 0 for fatal flaws.
  • Uses high-level rubrics, similar to how expert mathematicians evaluate proofs.

• Meta-verifier

  • Checks if the issues identified by the verifier are legitimate.
  • Prevents hallucinated issues where the verifier claims problems that do not exist.
  • Improves verifier faithfulness from 85 to 96.

• Proof generator

  • Generates mathematical proofs.
  • Trained using the verifier as its reward model.

This creates an iterative improvement loop. The verifier improves the generator through feedback. As the generator produces harder proofs, those challenges become training data that enhance the verifier itself.

Key Innovation

Instead of requiring human experts to label every proof, the system:

• Produces multiple verification analyses per proof.
• Uses meta-verification to validate identified issues.
• Routes ambiguous cases to human experts.

Human involvement remains part of the pipeline, but the bulk of verification is automated and self-improving.

Prompt Design That Sets a Standard

The prompt template from the paper is a standout. It shapes behavior before the problem is even presented and enforces a strict standard for what a valid solution must look like.

Here is the structure the prompt enforces:

• Define the task
  • Solve the given problem.
• Set expectations before the problem
  • Specify how reasoning should proceed at a high level.
  • Define what a final solution should include and how it should be formatted.
• Add evaluation and scoring
  • Instruct the model to evaluate its own solution.
  • Score the solution according to clear criteria.
• Ground the process
  • Add extra requirements tied to the nature of the problem.
  • Ensure every step is grounded and auditable.
• Establish self-assessment
  • Remind the model that it can rate its own solution due to reinforcement learning with verifiable rewards.
• Define final response constraints
  • Provide an exact template for the final response.
• Provide fallback and worst-case plans
  • Offer backup routes if the main reasoning path fails.
  • Describe what a worst acceptable final plan would look like.
• Only then, present the problem

Adopting this structure for coding and math tasks that require deep analysis is a valuable takeaway.

Why This Approach Matters

• It redirects focus from answers to reasoning
  • The target is not just getting the correct final answer but producing a proof that stands up to scrutiny.
• It trains for verifiability
  • The model develops the habit of checking and scoring its own work with consistent criteria.
• It supports trustworthy systems
  • Correct-by-construction reasoning benefits fields like software verification, cryptography, and systems design.

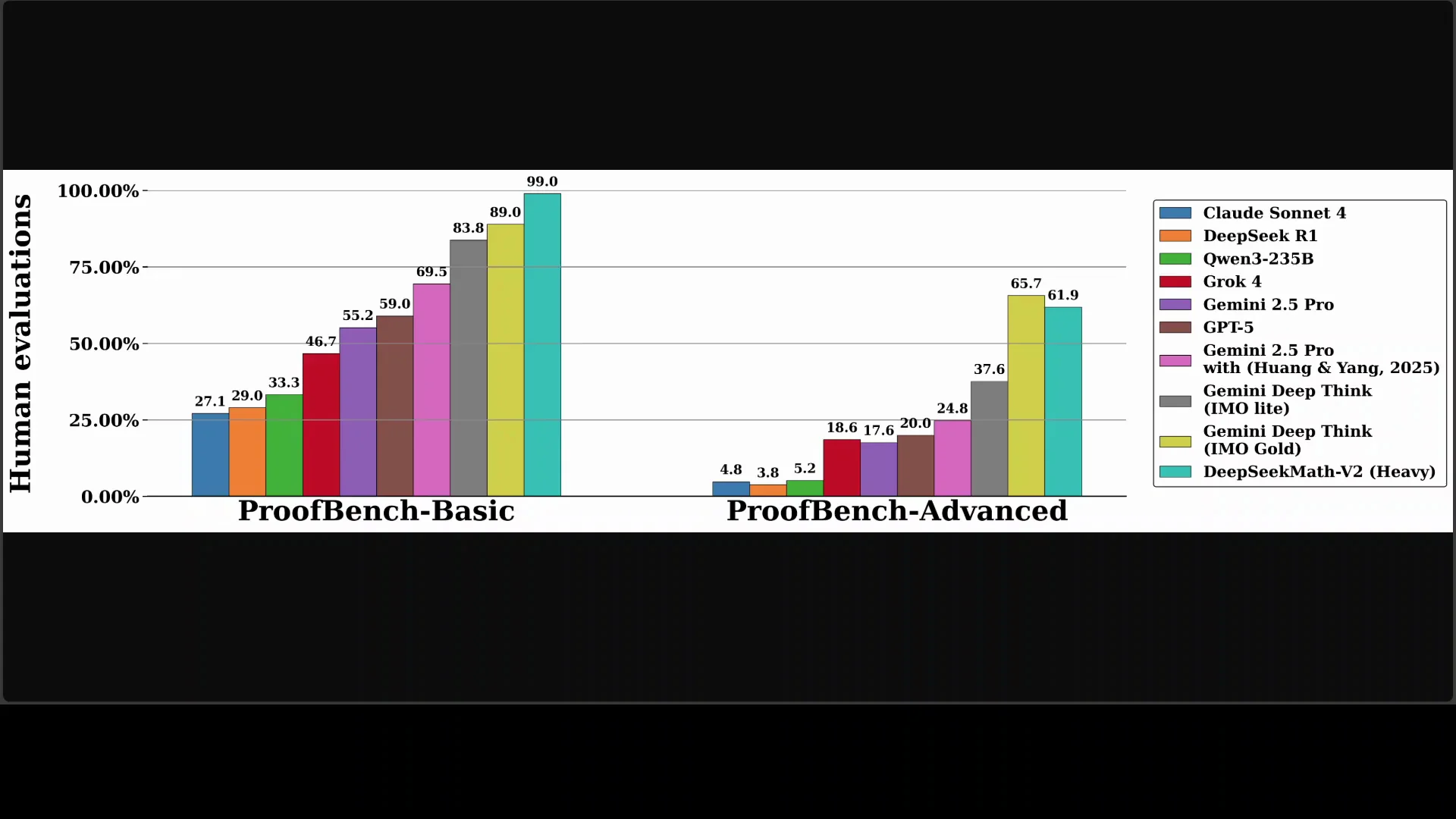
Benchmarks: What DeepSeekMath-V2 Achieves

The results reported are notable across key evaluations:

• International Mathematical Olympiad
  • Solved 5 of 6 problems.
  • Achieved gold medal performance at 83.3 percent.
• China Mathematical Olympiad 2024
  • Reported successful problem solving.
• Putnam 2024
  • Reported strong performance.
• ProofBench
  • Two subsets: Basic and Advanced.
  • Basic set success rate: 99.0 percent.
  • Advanced set success rate: 61.9 percent.
  • Substantially outperformed baselines including GPT-5, Gemini, Claude Sonnet 4, and others.

Here is a compact summary:

Benchmark	Reported Outcome
International Mathematical Olympiad	5 of 6 problems solved, 83.3 percent gold status
China Mathematical Olympiad 2024	Reported successful problem solving
Putnam 2024	Reported strong performance
ProofBench Basic	99.0 percent success
ProofBench Advanced	61.9 percent success
Baselines	Outperformed GPT-5, Gemini, Claude Sonnet 4, others

Test-time Compute Scaling

For the hardest problems, the model scales up compute at test time:

• Generates 64 initial proof candidates.
• Runs 64 verification analyses.
• Selects outputs based on verification, improving odds of a rigorous solution.

This test-time strategy helps push performance on the most challenging tasks.

From Answers to Verifiable Reasoning

If I summarize the shift, it moves from get the right answer to construct verifiable reasoning. Teaching AI to evaluate and improve its own mathematical arguments is a crucial step toward trustworthy and capable reasoning systems. That, in turn, shapes how we approach complex problems across science, engineering, and technology, which underpin industrial progress.

Availability and Next Steps

I tried to find this model on DeepSeek chat and other providers. I could not see it being served yet. I would have tested it if it were accessible. I will try it as soon as I get access.

The Case for a Math-First Model

DeepSeek releasing a math-focused model has sparked debate. The size is immense at 163 shards, and most cannot run it locally. Still, the release is important. AI is not only about user-facing features or broad text generation. A math model is a strategic bet on reasoning.

I am not running it locally. My goal here is to explain why it matters and what is new in DeepSeekMath-V2. I will keep things direct and useful.

Why Mathematical Reasoning Sets the Bar

• Precision is non-negotiable
  • One incorrect step can invalidate an entire proof.
• Logical soundness is the product
  • Proofs are not just outputs. They are structured arguments that must hold together.
• It is the right benchmark
  • Mathematics exposes flaws in reasoning. That is what we need to test and improve in AI.

A Prompt That Teaches the Model to Think

The prompt in the paper is deliberate and layered. It designs the thinking process before the question arrives.

• It frames the problem-solving approach.
• It sets the structure of the final answer.
• It includes evaluation criteria and self-scoring.
• It adds fallback and worst-case paths.
• It keeps everything grounded in the original problem.

This is worth adopting for research-heavy tasks, coding, or any problem that needs deep analysis and a defensible output.

What Earlier Math Models Missed

Earlier math-focused efforts optimized for end answers with reinforcement learning rewards. That led to:

• Correct outputs with broken reasoning.
• Invalid proofs filled with inconsistencies.
• Self-verification failures, including hallucinated claims of correctness.

DeepSeekMath-V2 aims at a different target: proof verification without requiring reference solutions. It builds the ability to spot errors the way mathematicians do, even without knowing the final answer.

The Dual System Plus Generator

• Verifier
  • Detects issues, scores rigor, and follows expert-style rubrics.
• Meta-verifier
  • Confirms that detected issues are real and reduces hallucinated findings.
  • Lifts verifier faithfulness from 85 to 96.
• Proof generator
  • Builds proofs and learns from verifier feedback as a reward model.

Together, they create a feedback loop that steadily increases rigor. As proofs get harder, verification also gets better.

Human-in-the-Loop Where It Matters

The system avoids asking humans to label every proof. It:

• Produces multiple analyses for each proof.
• Runs a second layer to check the first layer’s findings.
• Sends unclear cases to human experts.

That keeps human time focused on the edge cases and builds a reliable training signal for the rest.

Benchmarks, Scaling, and Takeaways

• Olympiad-level capability
  • Five of six IMO problems solved and gold-level performance at 83.3 percent.
• Strong signals across competitions
  • Reported successes on China Mathematical Olympiad 2024 and Putnam 2024.
• ProofBench rigor
  • 99.0 percent on the Basic set and 61.9 percent on the Advanced set.
  • Clear gains over baselines such as GPT-5, Gemini, and Claude Sonnet 4.

Test-time scaling helps on the toughest problems:

• 64 proof candidates.
• 64 verification analyses.
• Selection guided by verification scores.

Step-by-Step: How DeepSeekMath-V2 Tackles a Proof?

1. Frame the task
   • Define how to think and what a complete solution must contain.
2. Generate candidates
   • Produce multiple proof attempts rather than a single path.
3. Verify rigor
   • Score each attempt on completeness, omissions, and fatal flaws.
4. Check the checker
   • Run meta-verification to confirm detected issues are real.
5. Select and refine
   • Choose the highest-scoring proof and refine as needed.
6. Human review for edge cases
   • Route ambiguous outputs to experts for resolution.
7. Feed back to training
   • Use hard cases to improve verifier and generator over time.

This cycle shifts focus from answer-seeking to building and validating sound reasoning.

Final Thoughts

For me, the standout idea is simple. Focus on verifiable reasoning, not just outputs. By training models to scrutinize their own mathematical arguments and improve them, we move closer to systems that can be trusted with complex, high-stakes work across science, engineering, and technology.

I will test the model as soon as I can access it. Until then, the paper’s approach, the prompt design, and the reported results already tell a clear story about where reasoning-focused AI is heading.